The leading idea of the work of the Comenius University (UBR) team is reduction of loss risk by analyzing optimization problems on Markov chain models. To construct the latter conditional probabilities based on observations have to be computed. Parallely, methods of information value assessment are being developed. Particular models concern several social benefit areas.
- Disaster: In cooperation with the IIASA team its model of forest fire prevention is being further developed by:
Calculation of optimal thresholds for the fire danger classes. The existing model uses fixed thresholds without any justification of their values. Optimization of thresholds leads to cost reduction.
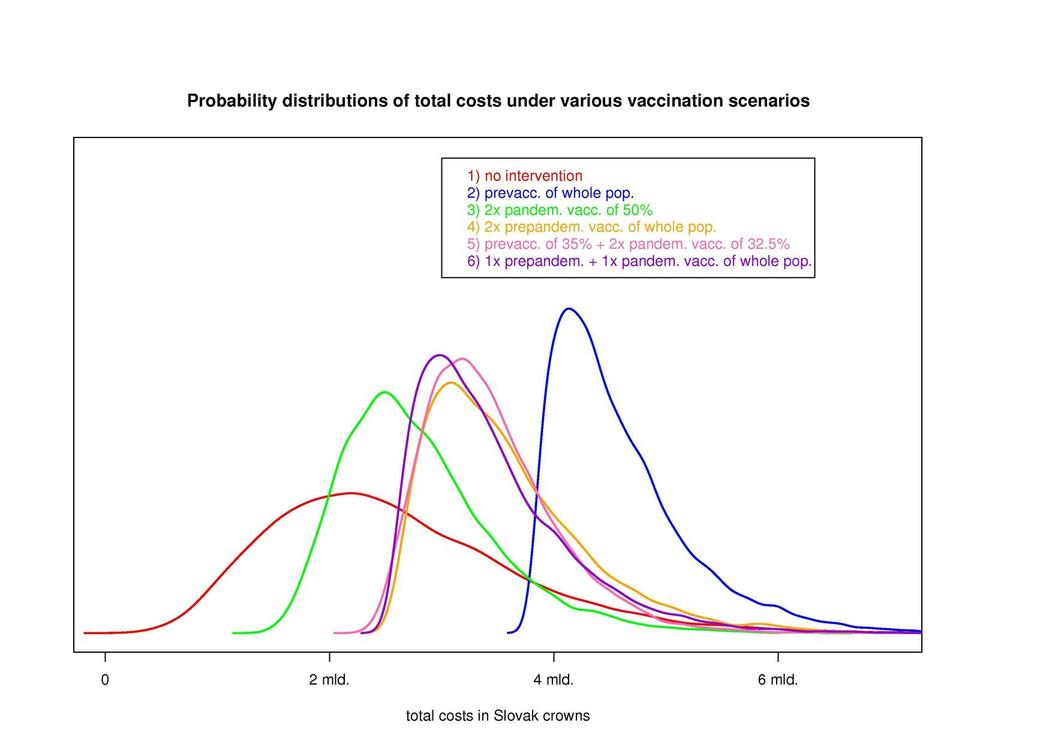
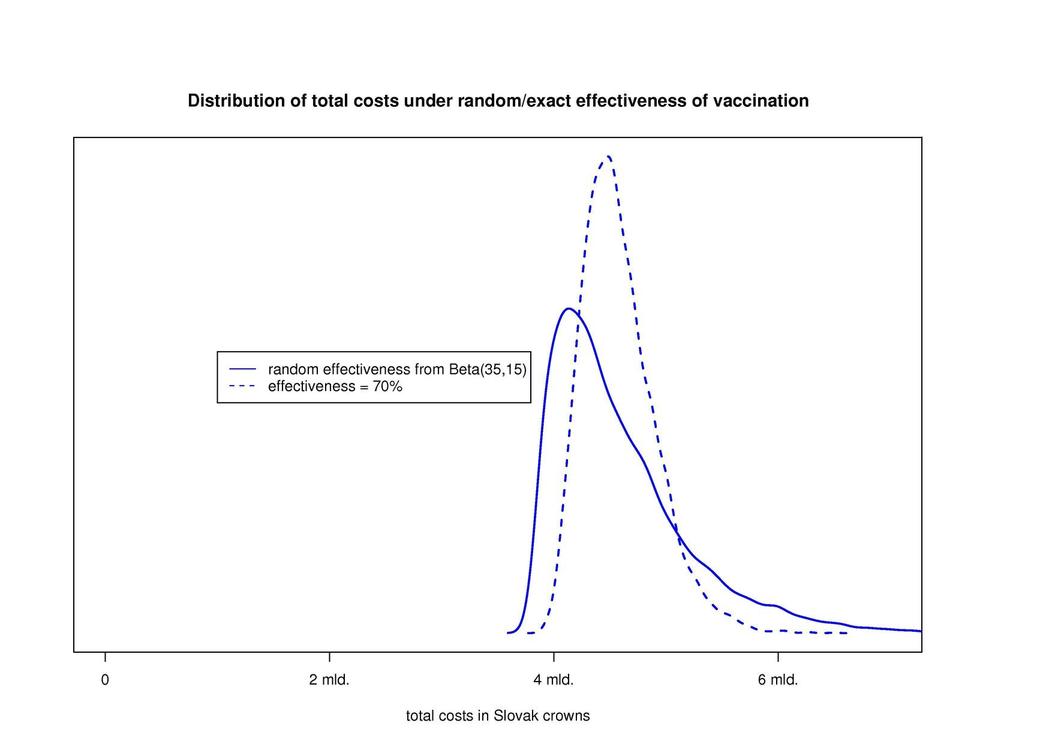
Application of the risk-based approach. So far, only the average values of the distribution have been considered. Therefore, the analysis of the properties of the distribution tails was impossible. The application of VaR and CVaR techniques appears to be promising. - Health: In cooperation with GlaxoSmithKline researchers a basic assessment of losses caused by a pandemic influenza has been worked out and is being further developed. The material will be submitted to the National Pandemic Committee of Slovakia. The first picture shows probability distributions of total costs under various vaccination scenarios. The second picture depicts a decrease of the variation of total costs provided using more precise data ( pre-vaccinaton effectiveness in particular). It serves as an example of benefit from related observations and research.
Figure: Probability distributions of total costs under various vaccination scenarios.
Figure: distribution of total costs under random/exact effectiveness of vaccination
Climate, Weather, Ecosystems: Decades long chains of data of daily precipitation, temperature and humidity values have been obtained from the Slovak Hydro-Meteorological Institute. To develop adaptive estimates of flood danger we developed a methodology of computing conditional probability of continuing rainfall after heavy rainfall days
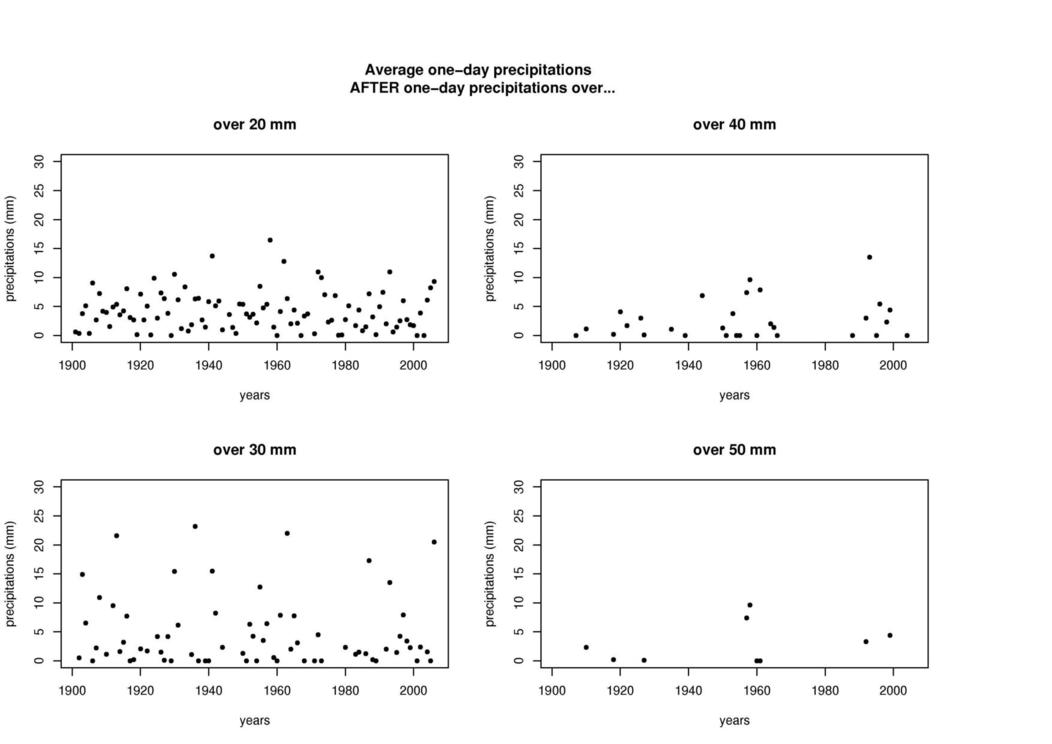
Figure: Average one-day precipitations AFTER one-day precipitations over...
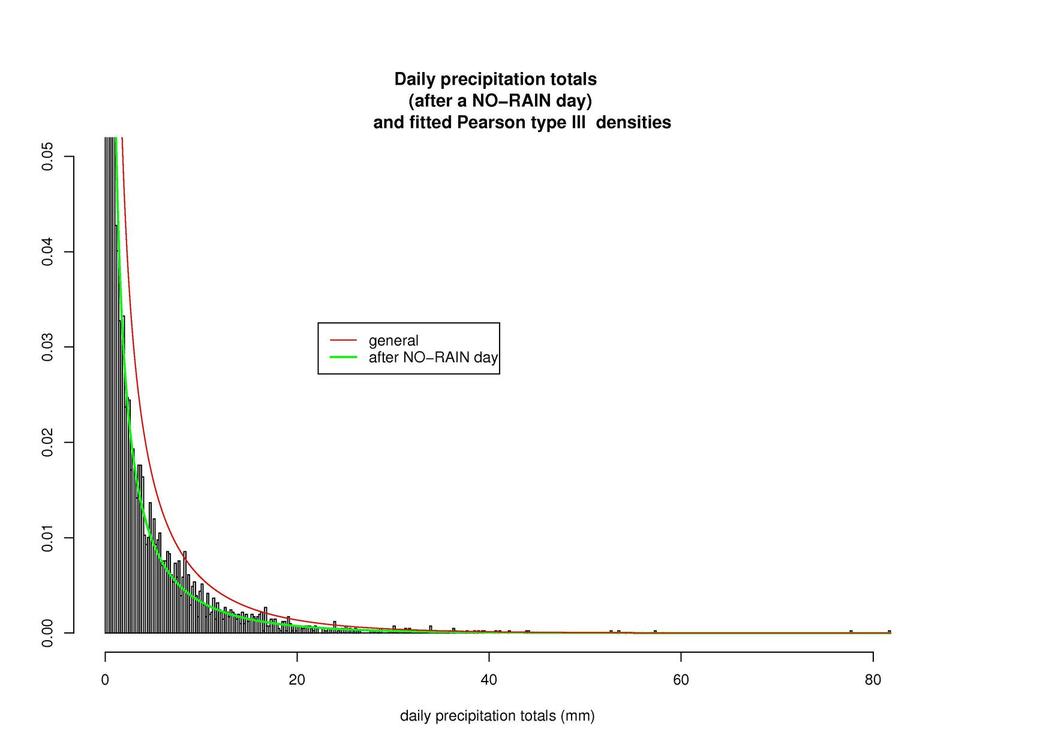
We also studied conditional probability distributions of rainfalls after specific events (e.g. after a no-rain day).
Figure: Daily precipitation totals (after a NO-RAIN day) and fitted Pearson type III densities
Currently we are working on an identification method of continuing extreme weather events, in particular of long periods without rainfall, high temperature and low humidity. From the results we expect to obtain some information on climate change and support of adaptive decision making based upon observations with help of an index similar to the used by the IIASA team for forest fire prevention.
In cooperation with the Institute of Hydrology of the Slovak Academy of Sciences a stochastic model of long-term prediction of the Danube river monthly discharge has been developed (Fig. P).. As a part of the project a similar autoregressive model of daily discharge is being developed. In combination with a transition matrix the model will enable to predict probability of flood events and their duration.